I’m starting a series called Learning JSF 2 on my blog. It will cover JSF 2 with emphasis on new features. Every post will cover a different features, the first one covers managed beans.
Managed bean is a regular Java bean with a fancy name. When we register the bean with JSF it becomes a managed bean, in other words, it’s now managed by the framework (JSF). In JSF, managed beans are used as model for UI components. In JSF 1.2, for a bean to become a managed bean, you had to register it in JSF configuration file such as faces-config.xml. One of the biggest announces was that as the number of beans grew, the JSF configuration file grew as well, and it was difficult to keep track of all names annd changes in three different files that all were “connected” (JSF configuration file, the JSF view and the bean itself).
Luckily, JSF 2 team has introduced annotations to register managed beans. With annotations, the bean and its registration are in the same place (Java class) so it becomes much easier to manage. You can still use JSF configuration file to register managed beans, and in some cases as you will see it’s the only way. Let’s start.
Basic Configuration
In JSF 1.2, the simplest registration looks like this:
userBean example.UserBean request
Exactly the same registration in JSF 2 looks like this:
package example;
import javax.faces.bean.ManagedBean;
import javax.faces.bean.RequestScoped;
@ManagedBean(name="userBean")
@RequestScoped
public class UserBean {
private String name;
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public UserBean() {}
}
JSF 2 introduces @ManagedBean and @RequestScoped annotations.
@ManagedBean – marks this bean to be a managed bean with the name specified in name attribute. If the name attribute in @ManagedBean is not specified, then the managed bean name will default to class name portion of the fully qualified class name. In this case it would be userBean. For example, this is the same as above:
@ManagedBean
@RequestScoped
public class UserBean {
...
}
@RequestScoped – sets the scope (request) into which this bean will be placed. If scope is not specified then bean will default to request scope. So we can write this:
@ManagedBean
public class UserBean {
...
}
My recommendation is to always write name and scope to make it easier to read and understand the code.
All scope annoations in JSF 2: @NoneScoped, @RequestScoped, @ViewScoped, @SessionScoped, @ApplicationScoped, and @CustomScope. @ViewScoped and @CustomScoped are new scopes in JSF 2 . I will cover @ViewScoped later in this post and @CustomScoped in another post.
@ManagedBean also has eager attribute (new in JSF 2). If eager=”true” and scope is application, then this bean must be created when the application starts and not during the first reference to the bean. In other words, the creation and storing of the bean instance must happen before any requests are serviced.
@ManagedBean(name="globalBean", eager=true)
@ApplicationScoped
public class GlobalBean {
...
}
If eager is true but scope is not application, then regular “lazy” initialization used. If eager is not defined or missing, then “lazy” initialization is used as well.
Using Managed Properties (or initialising bean properties)
To mark a bean property to be managed property, @ManagedProperty annotations is available:
@ManagedProperty(value="Mia") private String name;
When the bean is created, ‘Mia’ will be passed to setName(..) method.
Dependency Injection
JSF is a basic Dependency Injection (DI) container and we can use annotations to inject objects. JSF offers setter method injection – this means the object will be passed into the setter. It is also static injection – meaning, the injection will happen only during bean creation (as opposed to Seam, where static and dynamic injection is possible).
Suppose we want to inject userManager into userBean:
@ManagedBean(name="userManager")
@SessionScoped
public class UserManager {
private List users;
public List getUsers() {
return users;
}
...
}
Notice that we are using EL for the ManagedProperty.
@ManagedBean(name="userBean")
@RequestScoped
public class UserBean {
@ManagedProperty(value="#{userManager}")
private UserManager userManager;
public UserManager getUserManager() {
return userManager;
}
public void setUserManager(UserManager userManager) {
this.userManager = userManager;
}
...
}
In JSF 1.2, this would look like this:
userBean
example.UserBean
request
userManager
example.UserManager
#{userManager}
Still Need JSF Configuration File
Annotations definitely make life easier, however, there are some cases where JSF configuration file is still needed when working with managed beans (Note: I’m only refering to managed bean configuration, not to such things as navigation, locales, etc).
When you want to initialise a property such as list or map, it is still can only be done in JSF configuration file.
public class UserBean {
private List hobbies;
private Map favoriteSites;
// gettter and setter for both fields...
}
JSF configuration file:
userBean example.UserBean request hobbies java.util.List Swimming Running Dancing JSF favoriteSites java.util.Map
You will see that we moved the entire bean configuration into JSF configuration file now. It’s not possible to register the bean via annotations and then create managed properties in JSF configuration file. If you use annotations and then register the bean in JSF configuration file, then the registration in JSF configuration file will overwrite the annotations one.
View Scope
View scope is new scope in JSF 2. It will keep the bean alive as long as you are staying on the same view (page). I blogged about view scope in RichFaces here that you can use today with JSF 1.2.
The bean is saved as an attribute of the JSF view. When the JSF view (its state) is saved, the bean is saved as well. When the view is restored, the bean is restored and placed back in request scope.
View scope is very handy when editing a page with a list of objects. For example:
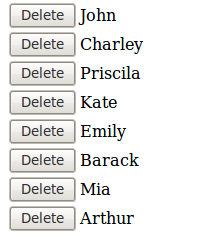
@ManagedBean(name="userList")
@ViewScoped
public class UserList {
private ArrayList users;
private String selectedUser;
@PostConstruct
public void create (){
users = new ArrayList ();
users.add("John");
users.add("Charley");
users.add("Priscila");
users.add("Kate");
users.add("Emily");
users.add("Barack");
users.add("Mia");
users.add("Arthur");
}
public void delete (){
users.remove(selectedUser);
}
public String getSelectedUser() {
return selectedUser;
}
public void setSelectedUser(String selectedUser) {
this.selectedUser = selectedUser;
}
public ArrayList getUsers() {
return users;
}
}
JSF view:
That’s it for the first entry in Learning JSF 2.
Leave a comment